9 minutes
Vector Gradient & Directional Derivative
Các thuật toán tối ưu hàm mất mát (loss function) phổ biến hiện nay như Gradient Descent hay Adam … đã cho thấy tính hiệu quả trong quá trình huấn luyện mô hình. Các thuật toán này hoạt động bằng cách cập nhật trọng số (weight) theo hướng ngược lại với vector gradient. Tại sao lại phải là ngược hướng Vector Gradient?
1) Ordinary derivative(đạo hàm thông thường)
Đạo hàm cấp 1 của hàm một biến ($f: \mathbb{R} \to \mathbb{R}$) (ordinary derivative) tại điểm $x$ được định nghĩa là : $$ f’(x) = \lim_{\Delta x \to 0} \frac{f(x - \Delta x) - f(x)}{\Delta x} $$ Công thức trên khá quen thuộc trong chương trình THPT . Nó biểu thị tốc độ thay đổi của $f(x)$ khi $x$ thay đổi một lượng rất nhỏ là $\Delta x$. . Đối với đồ thị trên mặt phẳng tọa độ, đạo hàm tại một điểm trên đồ thị bằng độ dốc của đường tiếp tuyến với đồ thị tại điểm đó. Chính vì thế mới có nguyên tắc tìm tiếp tuyến của đồ thị tại một điểm bằng cách tính đạo hàm.
$f’(x)$ luôn cho ta một hàm thuộc không gian 1 chiều ($f: R \to R$) . Hướng của nó được quyết định bởi dấu của $f’(x)$:
- Khi $f’(x) > 0$, hàm số đang tăng khi ta đi từ trái sang phải (hướng dương).
- Ngược lại $f’(x)$ < 0 hàm số đang giảm khi ta đi từ phải sang trái (hướng âm)
Nó chỉ thể hiện được độ dốc khi đi theo trục $x$. Vậy với không gian nhiều chiều thì sao ?
2) Vector Gradient, Directional Derivative
Trong không gian nhiều chiều chúng ta cũng cần tính độ dốc tại một điểm, nhưng lúc này điểm đó có nhiều tọa độ (ví dụ $(x,y)$ trong không gian 3 chiều với bề mặt $z = f(x,y)$ và độ dốc phụ thuộc vào hướng mà bạn di chuyển) Hãy tưởng tượng bạn đang đứng trên một sườn núi:
- Tại điểm mà bạn đang đứng nếu bạn bước sang ngang (theo đường đồng mức),độ dốc bằng 0 (giữ nguyên tọa độ $x, y$ thay đổi $z$)
- Nếu bạn bước thẳng lên đỉnh núi độ dốc sẽ lớn nhất (dương).
- Nếu bạn bước thẳng xuống chân núi , độ dốc cũng lớn nhất nhưng theo chiều âm.
- Nếu bạn bước theo một hướng chéo, độ dốc sẽ có một giá trị nào đó ở giữa.
Để giải quyết vấn đề này chúng ta có khái niệm Gradient (hay vector gradient)
2.1) Đạo hàm riêng (partial derivative)
Đạo hàm riêng (partial derivative) cũng hoạt động trên nguyên tắc của đạo hàm cấp một. Nhưng lúc này đạo hàm được tính riêng cho từng biến và xem biến còn lại là hằng số .Ví dụ hàm: $$f(x, y) = x^3y^2$$

- Đạo hàm hàm $f$ theo biến $y$, lúc này xem $x$ là hằng số. Ký hiệu $\frac{ \partial(f)}{\partial(y)} = x^32y^3$
- Đạo hàm hàm $f$ theo biến $x$, lúc này xem $y$ là hằng số. Ký hiệu $\frac{ \partial(f)}{\partial(x)} = 3x^2y^3$
Khi xem $x$ là hằng số, ta sẽ dùng một mặt phẳng, chẳng hạn $x=1$, để cắt đồ thị $z=x^3y^2$ , để lại giao tuyến là đường $1^3y^2 = y^2$
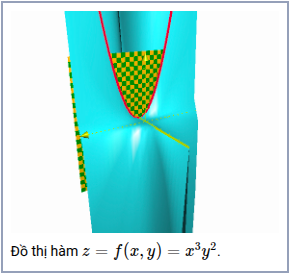
Việc dùng đạo hàm riêng cho chúng ta biết khi giữ nguyên một biến và thay đổi biến còn lại thì hàm số thay đổi bao nhiêu.Để có được thông tin về tốc độ thay đổi của hàm, chúng ta cần biến được gữ nguyên và thay đổi biến nào và có giá trị giữ nguyên là bao nhiêu Sau đó thay các giá trị này vào.
Với ví dụ trên ta có đạo hàm riêng theo biến $y$ của đại lượng $z$ khi $x = 1$.Tại điểm $(1, 2)$ ta có đạo hàm riêng theo biến $y $là $2y = 2\times2 = 4$ .Tức tại điểm đó $(1, 2)$ nếu ta giữ nguyên $x$ và thay đổi $y$ một lượng nhỏ là $\partial(y)$ thì $z$ thay đổi lượng gấp 4 lần khi ta thay đổi $y$ hay ta viết $\frac{\partial(z)}{\partial(y)}$ tại điểm đó là $4$
2.2) Vector Gradient
Thay vì tính đạo hàm riêng cho từng biến một cách riêng lẻ, chúng ta có thể sử dụng một đối tượng duy nhất gọi là vector gradient. Vector này tổng hợp tất cả thông tin về độ dốc (slope) của hàm số tại một điểm cụ thể, giúp quá trình tính toán trở nên hiệu quả hơn rất nhiều. Gradient của hàm $f(v)$ với $v = [v_1, v_2 … v_n]$ cũng là một vector ký hiệu là: $$ \nabla{f} = \begin{bmatrix} \frac{\partial(f)}{\partial(v_1)} \\ \frac{\partial(f)}{\partial(v_2)} \\ \frac{\partial(f)}{\partial(v_3)} \\ … \\ \frac{\partial(f)}{\partial(v_n)} \end{bmatrix} $$
Vector gradient có hai tính chất cực kỳ quan trọng, lý giải tại sao các thuật toán Gradient Descent lại cập nhật tham số (weights) theo hướng ngược lại với nó:
- Hướng (Direction): Vector gradient luôn chỉ về hướng mà tại đó hàm số tăng nhanh nhất (hướng dốc nhất).
- Độ lớn (Magnitude): Độ lớn của vector gradient cho biết tốc độ tăng trưởng lớn nhất của hàm số theo hướng đó.
Trong các bài toán học máy, mục tiêu của chúng ta là tối thiểu hóa hàm mất mát (loss function). Vì vector gradient chỉ ra hướng làm cho hàm số tăng nhanh nhất, nên để giảm giá trị của hàm mất mát, chúng ta cần di chuyển theo hướng ngược lại. Nguyên lý “đi ngược lại hướng dốc nhất” này chính là nền tảng cốt lõi của các thuật toán thuộc họ Gradient Descent.
Chúng ta sẽ chứng minh 2 tính chất trên vào cuối bài viết sau khi triển khai directional derivative.
2.3) Directional derivative(đạo hàm theo hướng)
Đạo hàm có hướng có nhiều ý nghĩa và chức năng khác nhau, trong bài này chỉ nói đến việc mô tả tốc độ thay đổi - độ dốc của hàm.
Đạo hàm có hướng là một dạng tổng quát của đạo hàm riêng. Nếu đạo hàm riêng chỉ có thể xét cho sự thay đổi của một biến thì đạo hàm có hướng xét sự thay đổi của nhiều biến.
Định nghĩa cơ bản nhất của đạo hàm theo hướng của hàm $f$ tại điểm $P(a, b)$ theo hướng của vector đơn vị $u(u_{1},u_{2})$ là một giới hạn, tương tự như đạo hàm một biến: $$ D_{u}(f(a,b)) = \lim_{h\to0} \frac{f(a+hu_{1}, b+hu_{2})- f(a,b)}{h} $$
- $h$ ở đây thể hiện khoảng cách thay đổi rất nhỏ theo hướng của vector $u$.Tưởng tượng bạn đang leo lên một đỉnh núi .Tại vị trí bạn đứng có tọa độ là $P(a, b)$, bây giờ bạn muốn đang đi với hướng của vector đơn vị $u$ thì $h$ chính là khoảng cách mà bạn bước . Vector dịch chuyển $hu = (hu_{1},hu_{2})$, điểm mà bạn đến có tọa độ là $(a+hu_{1}, b+hu_{2})$
Tính toán giới hạn trên thuờng rất phức tạp . Chúng ta cần một cách hiệu quả hơn.Hãy tưởng tượng bề mặt $z = f(x,y)$. Thay vì nhìn toàn bộ bề mặt ,chúng ta chỉ quan tâm đến những gì xảy ra dọc theo một đường thẳng đi qua điểm $P(a,b)$ theo hướng $u$.(tức là xem xét lát cắt chứa điểm đó và vector u thuộc 2 chiều )
Ta có thể định nghĩa đường thẳng này bằng tham số t:
- $x(t) = a + tu_1$
- $y(t) = b + tu_2$
Lúc này hàm $g(t) = f(x(t), y(t)) = f(a+tu_1, b+tu_2)$ là giá trị của f dọc theo đường thẳng này
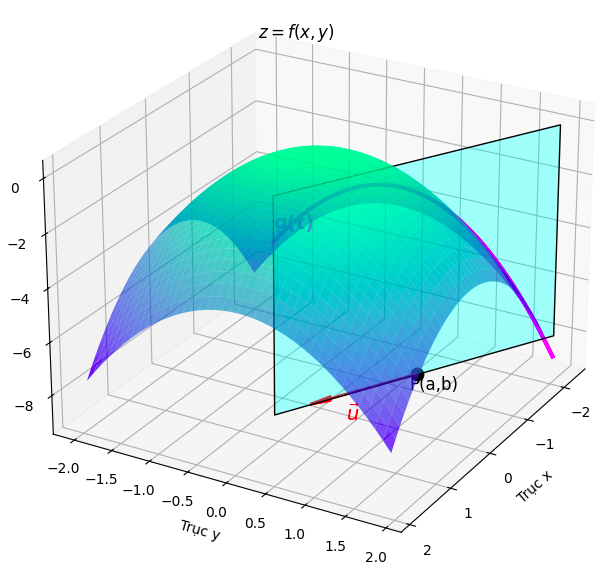
Hàm $g(t)$ là hàm một biến theo , $\frac{\Delta{g(t)}}{t}$ cho ta biết tốc độ thay đổi của $f$ dọc theo đường thẳng mà ta đã chọn.
Ta có: $$ g’(0) = \lim_{h \to 0}\frac{g(0+h) - g(0)}{h} = \lim_{h \to 0}\frac{g(h)-g(0)}{h} = \lim_{h \to 0} \frac{f(a+hu_1, b+hu_2)-f(a,b)}{h}=D_u{f(a,b)} $$ Mặt khác áp dụng quy tắc chain rules cho hàm 2 biến ta có: $$ g’(t)=f’(x(t),y(t))= f(a+tu_1, b+tu_2)= \frac{\partial{f}}{\partial{x}}\frac{d_x}{d_t} + \frac{\partial{f}}{\partial{y}}\frac{d_y}{d_t} =\frac{\partial{f}}{\partial{x}} u_1+ \frac{\partial{f}}{\partial{y}}u_2 $$
Ta có vector gradient là $: \Delta{f} = \begin{bmatrix} \frac{\partial(f)}{\partial(x)} \ \frac{\partial(f)}{\partial(y)} \end{bmatrix}$ hay $g’(t)$ = $\Delta{f}u$ vậy $g’(0)$= $\Delta{f(a, b)}u$. Nên ta có công thức tính đạo hàm hướng của vector đơn vị u: $$ D_u{f(a,b)} = \Delta{f(a,b)u} $$
Chứng minh 2 tính chất của vector gradient:
- Khi $f$ có độ dốc lớn nhất thì $D_u{f}_ = \Delta{f.u}$ là lớn nhất với $\Delta{f}$ và $u$ là 2 vector cùng chiều .Ta có công thức tính tích vô hướng của 2 vector : $$ \Delta f \cdot u = |\Delta f| , |u| , \cos\theta $$
Do $u$ là vector đơn vị nên $|u|= 1$ khi đó: $$\max (\Delta f \cdot u) =\max( |\Delta f| ,.\cos\theta)$$ Xảy ra khi $\Delta f{\max}$ là và $\cos\theta=1$ hay Vector Gradient cùng hướng với $u$ và có độ lớn là $\max$
Ý nghĩa: Đạo hàm có hướng là một dạng tổng quát của đạo hàm riêng. Nếu đạo hàm riêng chỉ có thể xét cho sự thay đổi của một biến thì đạo hàm có hướng xét sự thay đổi của nhiều biến.
Giả sử hàm $f: R^2 \to R$ nhóm các biến đầu vào thành một vector (khác với vector gradient là nhóm các đạo hàm riêng), tức là thay vì ghi $z = f(x, y)$ thì ghi $z = f(v)$ và ngầm hiểu rằng $: v = \begin{bmatrix} x \ y \end{bmatrix}$
Do có 2 biến $x, y$ nên không gian input là 2 mặt phẳng và không gian output của hàm $f$ là một tia số. Hàm $f$ “nối” một điểm trong không gian input chiều sang một điểm trong không gian output
Giả sử có một vector $w = (1, 3)$ chúng ta cầnchuẩn hóa nó thành vector đơn vị $u$ (vì vector đơn vị chỉ mang thông tin về hướng không quan trọng độ lớn ) . Vậy nếu chúng ta dịch chuyển điểm trong không gian input đi theo hướng của vector $u$ thì trong không gian output điểm đó bị đẩy đi bao nhiêu lần? Quan sát hình sau. Hai điểm cùng màu là một bộ input-output tương ứng nhau cho hàm $f$. Ví dụ ở bên trái, điểm màu đỏ $(1,2)$ làm input thì sẽ cho điểm màu đỏ ở ảnh phải có giá trị $f(x,y)=x^3y^2=4$. Bây giờ nếu trong hình trái, ta dời điểm màu đỏ sang vị trí điểm màu xanh theo hướng (chỉ hướng thôi nhé, còn khoảng cách được quyết định bởi $(h \to 0)$ của $w=(1,3)$, thì ở hình bên phải độ dời đó sẽ gấp bao nhiêu lần so với bên trái?
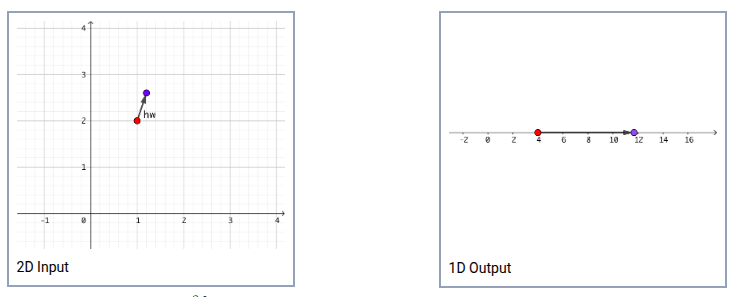
Ta có :
$$ u= \frac{w}{|w|} = (\frac{1}{\sqrt{10}}, \frac{3}{\sqrt{10}}) $$
$$ \Delta_uf(v) = \Delta{f} . u = \frac{1}{\sqrt{10}} . (3x^2y^2) + \frac{3}{\sqrt{10}} . (2x^3y) = \frac{1}{\sqrt{10}}.(3.1^2.2^2) + \frac{3}{\sqrt{10}} . (2.1^3.2) $$
Hay hình bên phải độ dời đó sẽ gấp $\frac{24}{\sqrt{10}}$ lần so với bên trái.Tại các điểm input cụ thể, ta có thể thay vào và tính ra được đạo hàm hướng tại điểm đó, còn gọi là tính độ dốc (slope).